定义

最简单的例子，常见的推荐有奖营销活动，如果需要找到最终的推荐人，那么就需要用到 递归。递归是一种应用非常广泛的算法或者是编程技巧。其中有两个难点：动态规划和递归。

递归需要满足的三个条件

1. 一个问题的解可以分解为几个子问题的解
2. 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
3. 存在递归终止条件

编写递归代码

编写递归代码关键在于 写出递推公式，找到终止条件。一个简单的例子：

假如这里有 n 个台阶，每次可以跨 1 个台阶或者 2 个台阶，请问走 n 个台阶有多少种走法？

仔细想一下，所有的走法可以分成两类，第一类是第一步走了 1 个台阶，另一类是第一步走了 2 个台阶。所以 n 个台阶的走法就等于先走 1 个台阶后，n-1 个台阶的走法加上先走 2 个台阶后，n-2 个台阶的走法，用公式表示就是:

$f(n) = f(n-1)+f(n-2)​$

当递推公式出来后，递归代码基本上就走了一半。终止条件和递推公式合并后就是：

1
2
3

f(1) = 1;
f(2) = 2;
f(n) = f(n-1) + f(n-2);

总结一下，写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

还有一点：编写递归代码的关键是，知道遇到递归，我们就把它抽象成一个递推公司，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

注意点

警惕堆栈溢出

递归代码需要重复调用自身的方法，当调用次数过大是，很有可能就会抛出堆栈溢出的异常。函数调用会使用栈来保存临时变量，每调用一个函数，都会临时变量封装为栈帧压入内存栈，等函数执行完成返回后，才会出栈。系统栈或者虚拟机控件一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

如何避免堆栈溢出的出现，最常见的办法就是使用循环遍历来替代递归，但是可读性可能会降低。后面会介绍例子。

警惕重复计算

如果把算台阶走法的题目分解一下，就是这样的：

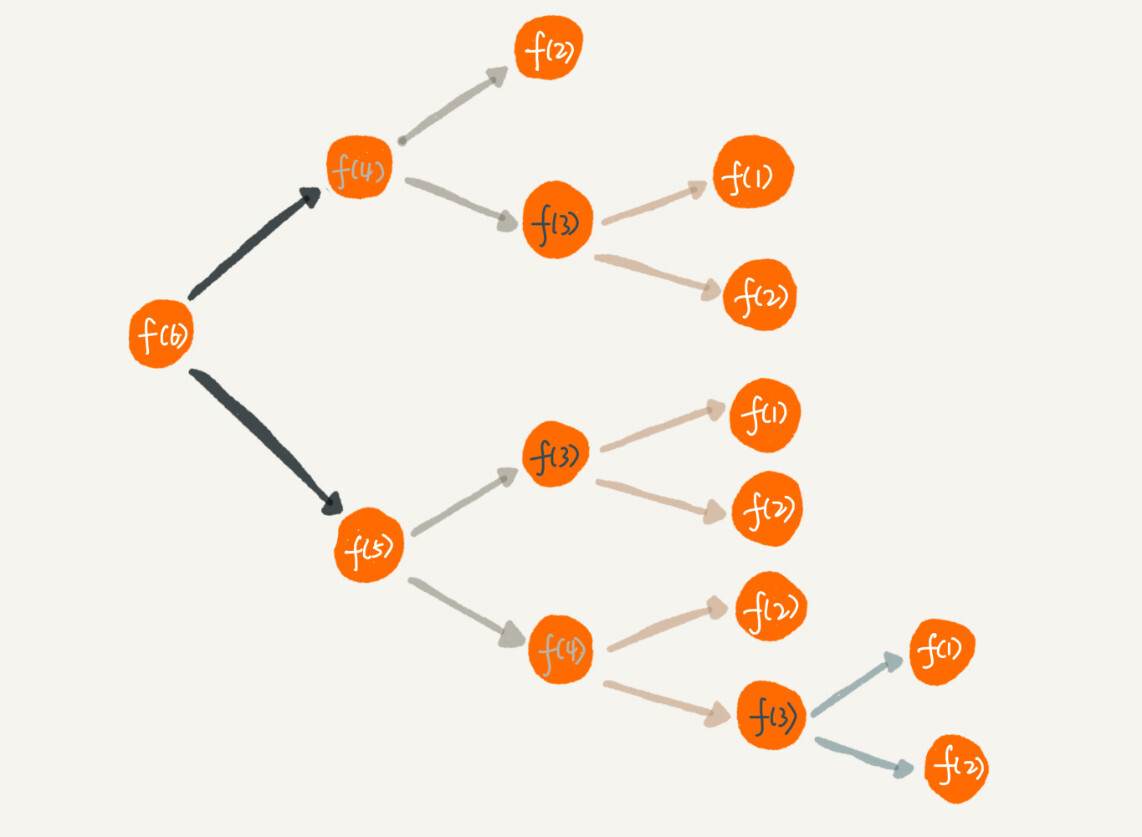
从图中可以发现有些是重复计算的，为了避免计算，就可以通过 HashMap 来保存计算的值，优化这个问题。

实战

首先使用普通的递归方式来实现台阶走法那个题目：

1
2
3
4
5

private int findLadder(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    return findLadder(n - 1) + findLadder(n - 2);
}

转换成循环迭代的方式：

1
2
3
4
5
6
7
8
9
10
11
12
13

private int findLadderNormal(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    int result = 0;
    int pre1 = 1;
    int pre2 =2;
    for (int i = 3; i <= n; i++) {
        result = pre1 + pre2;
        pre1 = pre2;
        pre2 = result;
    }
    return result;
}

在递归的基础上，优化重复计算：

1
2
3
4
5
6
7
8
9
10

private int findLadderAdvanced(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    if (cached.containsKey(n)) {
        return cached.get(n);
    }
    int result = findLadderAdvanced(n - 1) + findLadderAdvanced(n - 2);
    cached.put(n, result);
    return result;
}

总结

递归是一种非常高效、简洁的编码技巧。只要满足三个条件的问题就可以通过递归代码来解决。

不过递归代码也比较难写、难理解。编写递归代码的关键就是不要把自己绕进去，正确姿势是写出递推公式，找出终止条件，然后再翻译成递归代码。

参考自极客时间