前言

终于进入排序了，这应该是大学课上学的第一个算法，当时学的还不是很成熟，只是当时学会了如何去写，并没有深究其原理和时间复杂度等细节信息，在之后不久就忘记怎么写了。其实在大部分的编程语言中，也提供了排序函数。

其实在项目中也会经常用到排序算法，就拿我之前在两日三日 K 线时，服务端不愿意计算，只能所有逻辑放在客户端来算， 这对客户端来说无疑是增加了难度。因为数据规模很大，如果算法不是很好的话，会浪费很多的时间在数据的计算上，尤其我们项目中的计算大部分是放在主线程中计算的，过长时间的计算，很大可能上会阻塞 UI 上的更新，造成卡顿，影响用户体验。

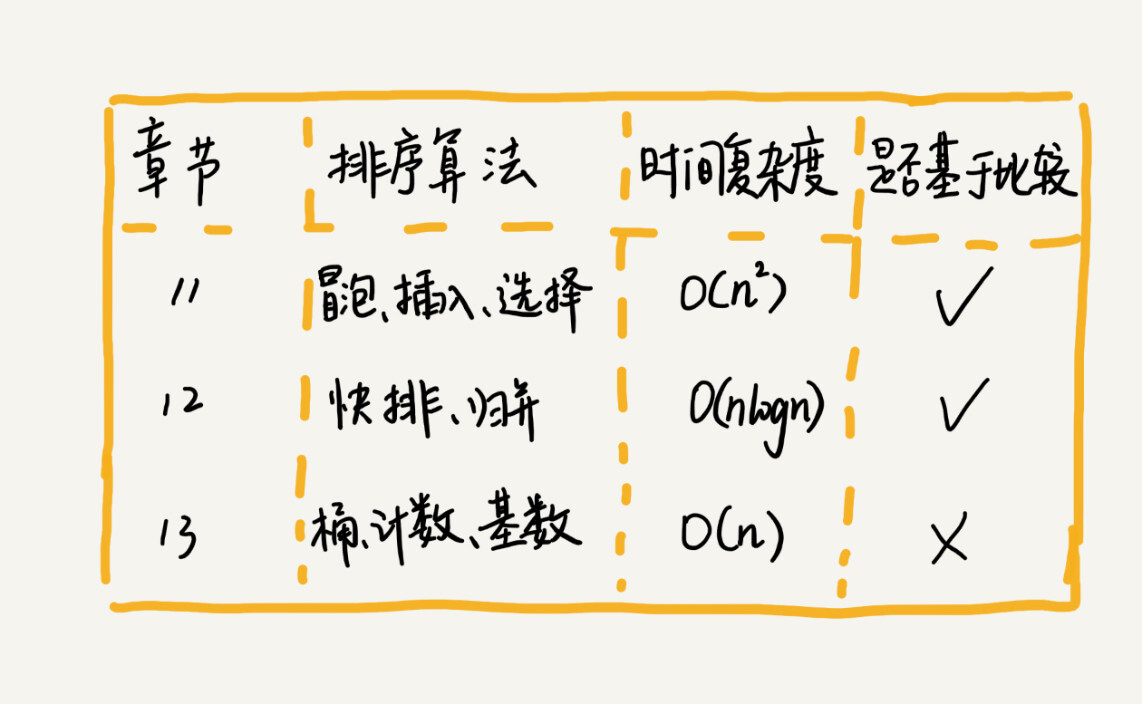
当然，排序算法也有很多种类，最经典最常用的有：冒泡、插入、选择、归并、快排、计数、基数排序、桶排序、按照时间复杂度可以分成三类：

如何分析排序算法

大学时只是学了如何写，现在要想学好排序，除了学习其原理和代码实现之外，更重的是要学会如何评价和分析一个排序算法。分析一个拍排序算法从以下三种方式入手：

排序算法的执行效率

1. 最好情况、最坏情况、平均情况时间复杂度

   要分析排序算法，就必须把这些因素全部考虑到。

2. 时间复杂度的系数、常数和低阶

   在算时间复杂度的时候，往往会把这三个因素忽略到，因为考虑到数据规模的无线庞大，那这几个因素的影响可以忽略不计。但在实际的项目中，数据规模是有限的，那么如何选择一个排序算法，就必须将这些因素重新放在考虑之中了。

3. 比较次数和交换(或移动)次数

   一切影响性能或者影响时间的因素都要放在考虑之中。

排序算法的内存消耗

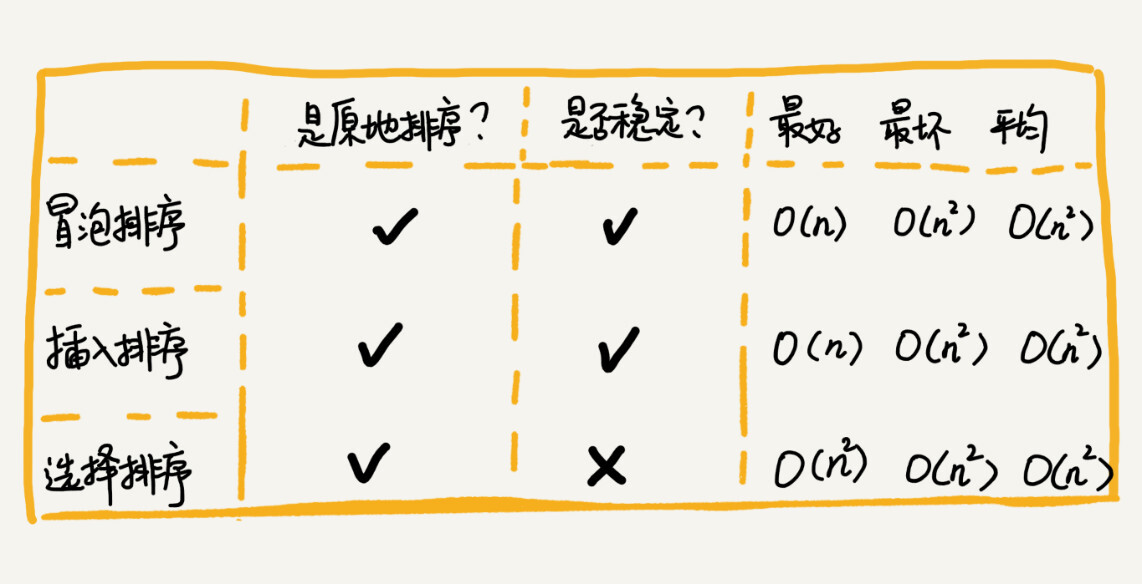
空间复杂度当然也是考量的标准，不过针对排序算法的空间复杂度，引入累计额一个新的概念，原地排序。原地排序算法，就是特指空间复杂度是 $O(1)$ 的排序算法。冒泡、选择和插入都是原地排序算法。

排序算法的稳定性

除了以上的标准外，还有一个因素需要被考虑进去，稳定性。简单来说，在排序中，对于相同元素（针对此次排序的 key 相同）来说，在进行排序后，还能保证原来的顺序，那么这个排序算法就叫做 稳定的排序算法。

稳定排序算法可以保持相同的两个对象，在排序之后的前后顺序不发生改变。

冒泡排序

冒泡排序只会操作相邻的两个数据，每次冒泡操作都会对相邻的两个元素进行比较，不满足则需要进行交换。来看第一次冒泡的详细过程。

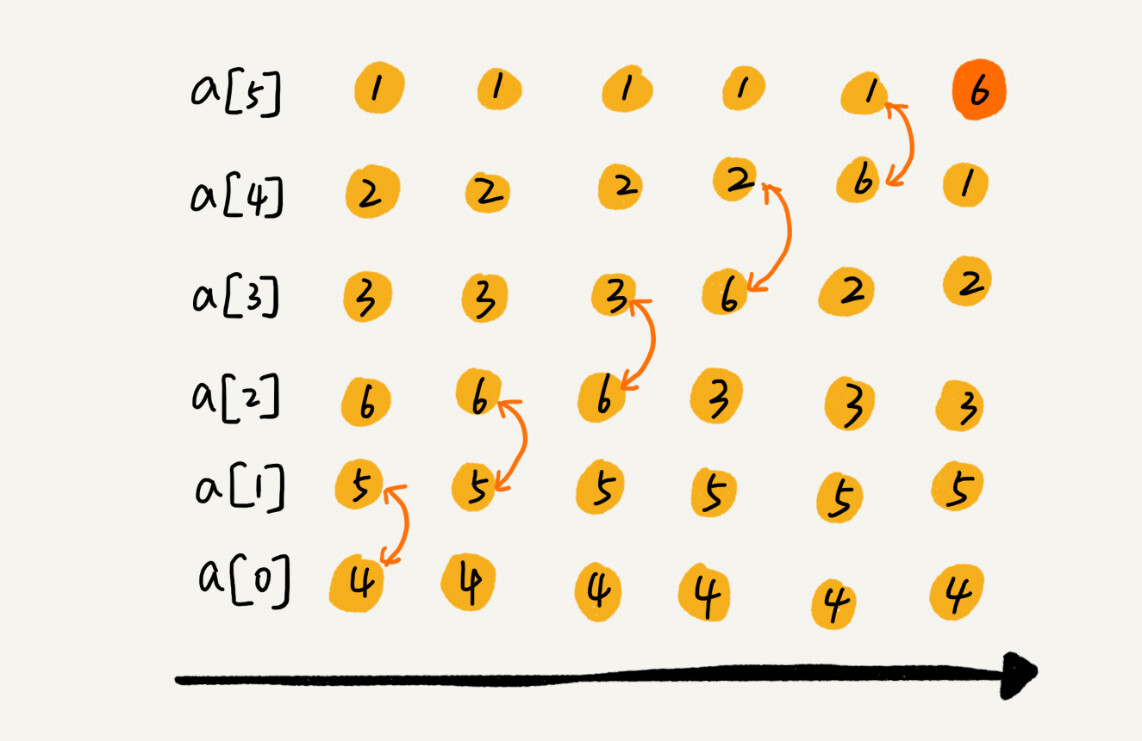
这么看来的话，一共需要 n 次冒泡，但是可以进行优化，如果某次没有交换，说明已经完全有序，就不需要进行冒泡。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

private boolean dataChanged = false;
private void bubbleSort(int[] data, int n) {
    if (n <= 1) return;
    for (int i = 0; i < n - 1; i++) {
        dataChanged = false;
        for (int j = 0; j < n - 1 - i; j++) {
            if (data[j] > data[j + 1]) {
                int temp = data[j + 1];
                data[j + 1] = data[j];
                data[j] = temp;
                dataChanged = true;
            }
        }
        if (!dataChanged) break;
    }
}

根据之前总结的排序算法特性，来看一下冒泡排序的特点：

1. 是原地排序算法

2. 是稳定的排序算法

3. 最坏时间复杂度 $O(n^2)$，最好时间复杂度 $O(n)$，平均时间复杂度 $O(n^2)$

   这里引入两个概念 有序度 和 逆序度。有序度 是数组中具有有序关系的元素对的个数，通常的表达式：有序元素对：a[i] <= a[j], 如果 i < j。

   满有序度 = $n*(n-1)/2$ ，满有序度=有序度+逆序度。

插入排序

插入排序的关键思想是将数组中的数据分为两个区间 已排序区间 和 未排序区间。初始已排序区间只有一个元素，每次从未排序区间取出一个元素，在已排序区间找到合适的位置插入，并保证已排序区间数据一直有序。

如何找到合适的位置插入？依次比较待插入的区间，不符合要求的进行数据迁移，直至找到满足条件的停止迁移。如图：

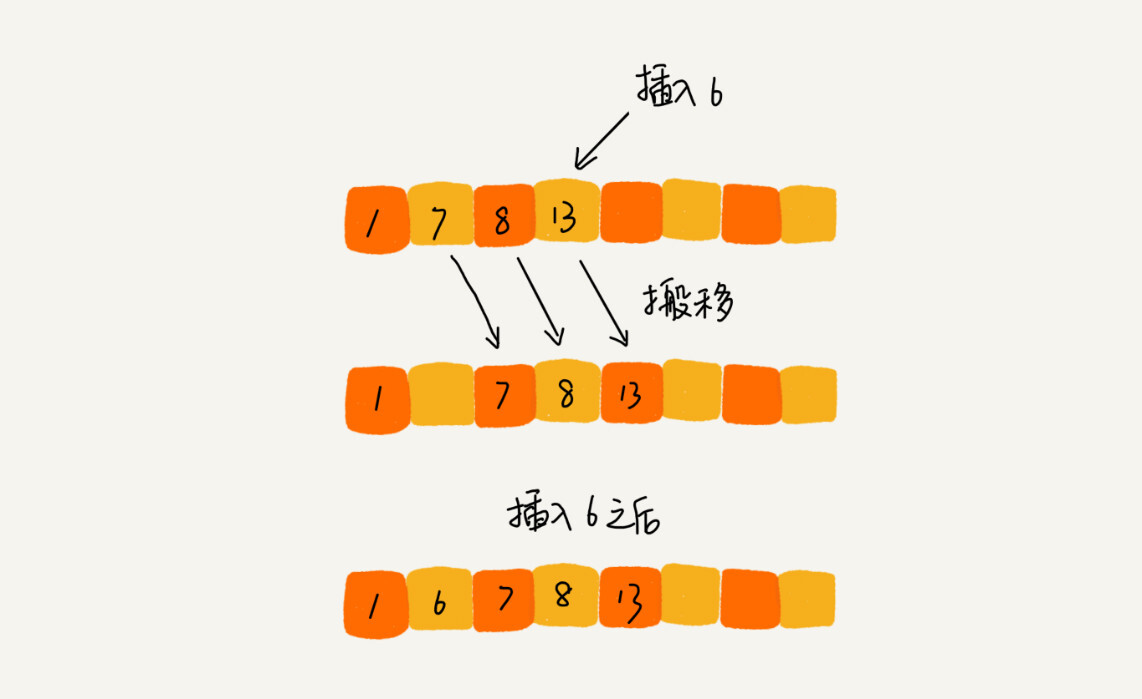
假设要排序的数据是 4,5,6,1,3,2,其中左侧是已排序区间，右侧是未排序区间。

整个过程包含两种操作， 元素的比较 和 元素的移动。用到上面说的有序度相关知识，数据移动的个数等于逆序度。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

private void insertSort(int[] data, int n) {
    if (n <= 1) return;
    for (int i = 1; i < n; i++) {
        int value = data[i];
        int j = i - 1;
        for (; j >= 0; j--) {
            if (data[j] > value) {
                data[j + 1] = data[j];
            } else {
                break;
            }
        }
        data[j + 1] = value;
    }
}

特点：

1. 是原地排序算法
2. 稳定的排序算法
3. 最坏时间复杂度 $O(n^2)$，最好时间复杂度 $O(n)$，平均时间复杂度 $O(n^2)$

选择排序

核心思想：每次找到最小的元素放置在已排序区间。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

private void selectSort(int[] data, int n) {
    if (n <= 1) return;
    for (int i = 0; i < n - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (data[j] < data[minIndex]) {
                minIndex = j;
            }
        }
        if (i != minIndex) {
            int temp = data[i];
            data[i] = data[minIndex];
            data[minIndex] = temp;
        }
    }
}

特点：

1. 是原地排序算法
2. 不是稳定的排序算法
3. 最好最坏都是 $O(n^2)$

总结

为了对比三者的时间复杂度，我构造了一个二维数组，作用在于随机创建 200 条 长度为 4000 的数据，用三种排序算法对其进行排序，对比他们的总耗时：

1
2
3
4
5
6
7
8
9
10

public static int[][] createRandomData(int count, int perNum) {
    int[][] data = new int[count][perNum];
    Random random = new Random();
    for (int j = 0; j < count; j++) {
        for (int i = 0; i < perNum; i++) {
            data[j][i] = (int) (random.nextDouble() * 1000);
        }
    }
    return data;
}

结果：

冒泡排序：3601ms

选择排序：1998ms

插入排序：694ms

数据越庞大，对比效果越明显，冒泡排序多了一个比较交换的操作，时间复杂度会高上一点，插入排序表现尤为出色，因此优先会选插入排序。最后看一下三者比较一览图：

参考自极客时间https://time.geekbang.org/column/126)