『数据结构与算法』—— 链表
字数统计:
2,839 字
|
阅读时长:
13 分
| 本文总阅读量: 次
底层存储结构
与 数组 对比,数组需要一块 连续的内存空间 来存储,对内存要求很高。如果我们申请 50MB 的内存,即便内存的剩余内存大于 50MB,但是如果内存不是连续的,也是很有可能申请失败。
而 链表 与之相反,它并不需要一块连续的内存,通过 指针 将一组 零散的内存块 串联起来使用。
下面的图片可以看出两者之间的区别:
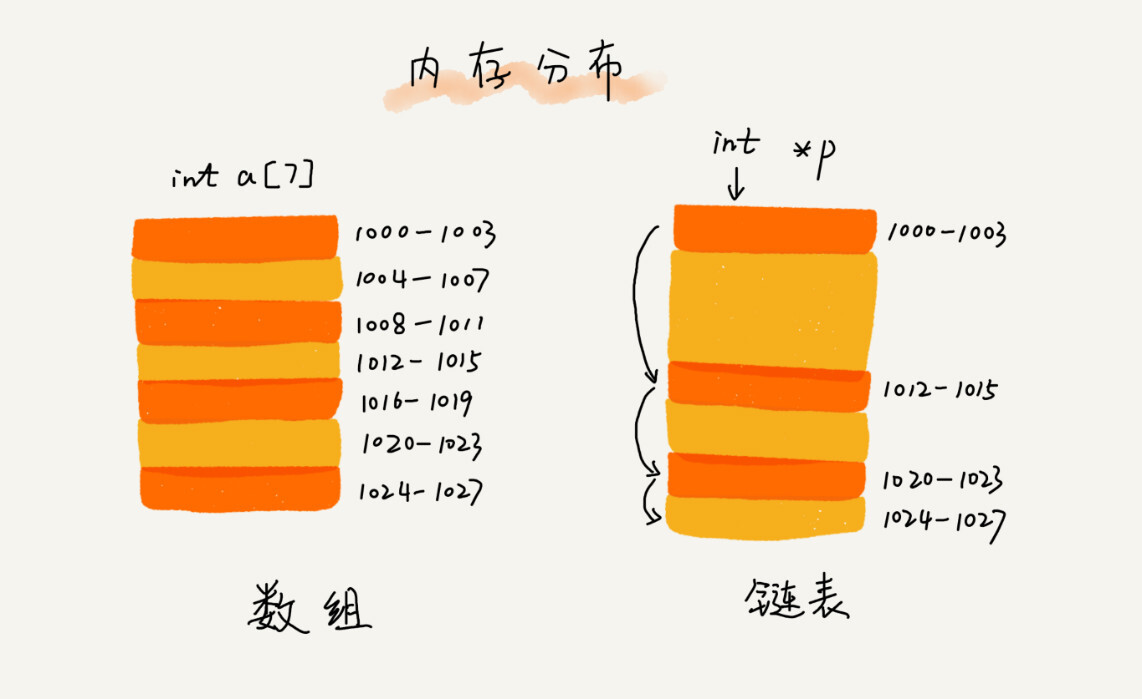
链表分类
单链表
单链表每个节点有两部分组成,数据 和 后继指针 next 。
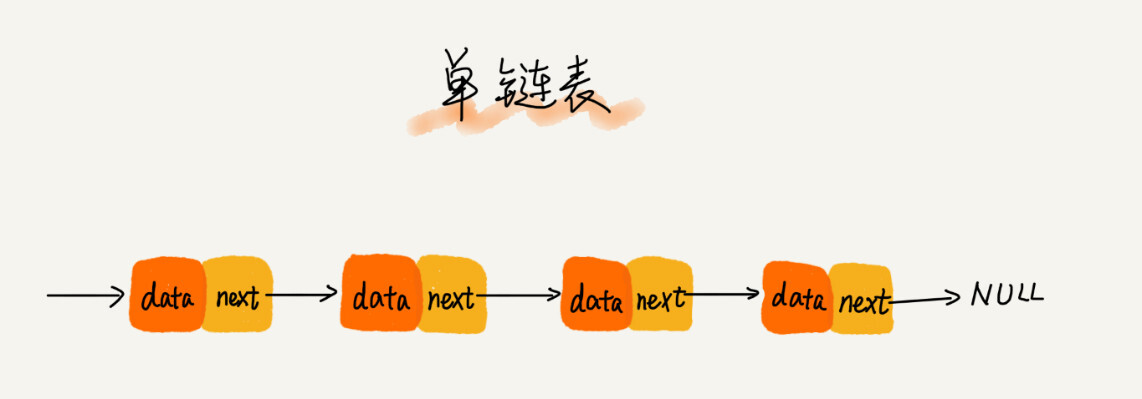
第一个节点称为 头结点, 最后一个节点称为 尾节点 ,尾节点 next 指向 null。链表的插入增加和删除,不需要移动,只需要改变前后节点 next 的指针即可实现。
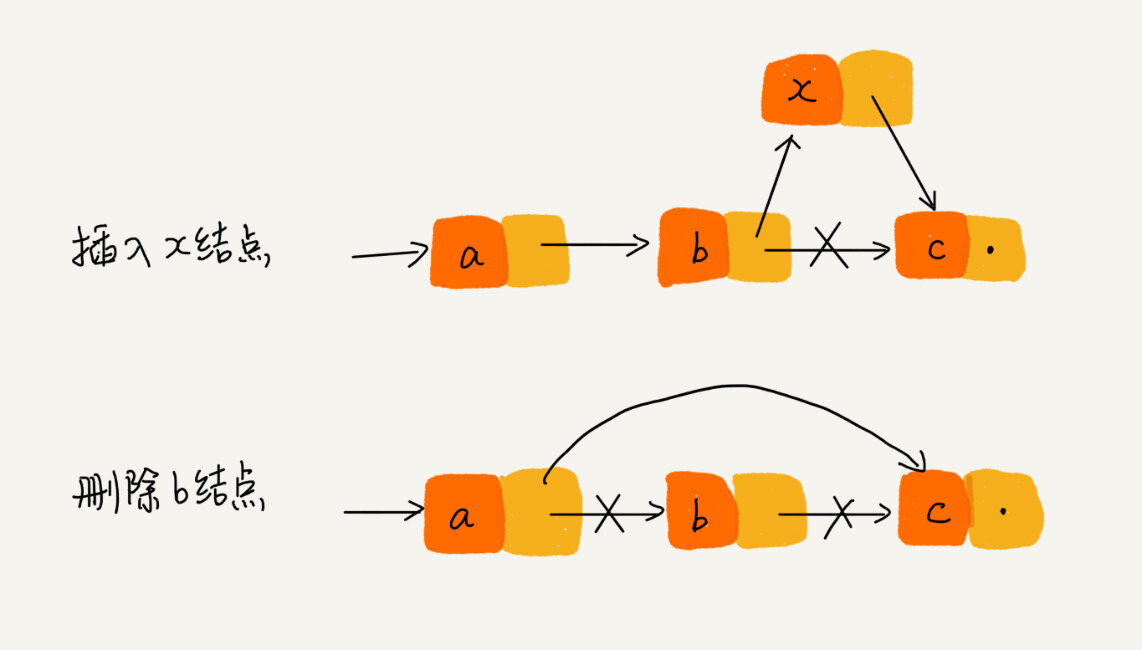
但是,如果需要访问第 N 个元素,则需要时间复杂度为 $O(n)$ 。
循环链表
循环链表是从链尾直接连接到链头。
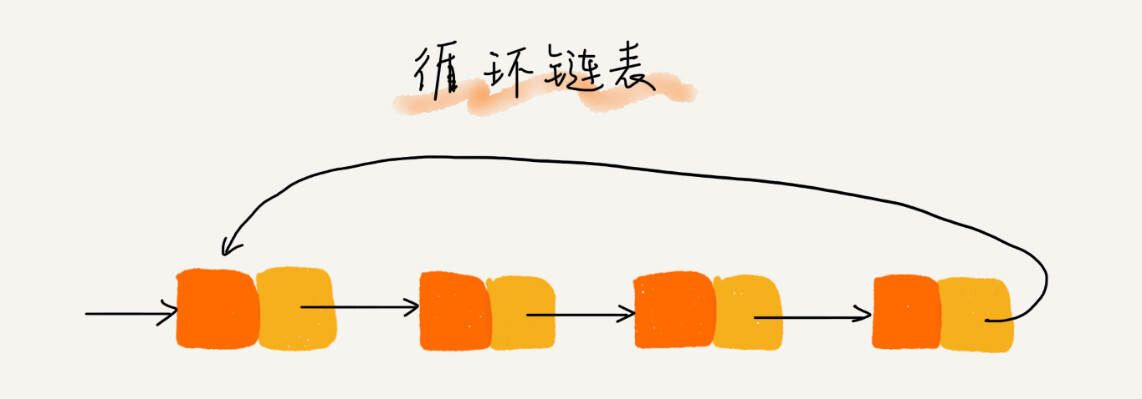
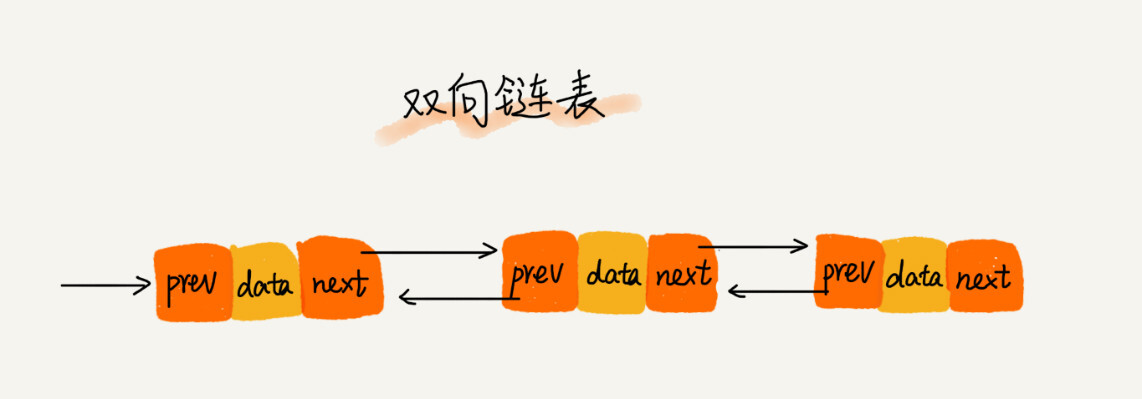
双向链表
相比于单链表,双向链表具有两个节点:前继节点和后继节点。
LRU 缓存淘汰算法
维护一个有序单链表,越靠近链尾的节点是越早访问的,当有一个新的数据访问时,我们从链表头部开始顺序遍历链表。
- 如果该数据已经存在于链表中,那么遍历拿个这个数据的节点删除,并将新的插入到头部。
- 如果此数据没有再缓存链表中:
- 如果缓存未满,则直接将该节点插入链表的头部
- 如果此时链表已满,则链表尾节点删除,将新的数据节点插入到链表的头部。
链表小总结
说一句尴尬的话,本人大学的时候也是挂了 算法与数据结构 这门课,说实话,对算法也是有一点阴影,总感觉自己会学不好。就拿写链表而言,经常被引用的移动产生误解,在过程中经常不知道指针移到到哪了,导致并不会实现自己预期想要的结果。其实练习题做下来还是蛮有感触的,还是要多练习,从中可以找到一些技巧,下面总结一下:
理解指针或引用的含义
对于我这个学习 Java 的而言,其实就是要理解引用的含义。
将某个变量赋值给引用,实际上是将这个变量的地址赋值给该引用,或者反过来说,引用中存储了这个变量的内存地址,指向了这个变量,通过这个指针就能找到这个变量。
例子
1
2
3
4
5
| Node node1 = new Node(null, 1);
node1 = new Node(null, 2);
Node node2 = new Node(null, 3);
node1 = node2;
node1.value = 3;
|
只要是 node = 引用后面直接跟上等于,那就证明只是单纯的将这个引用指向另一个内存地址,并不会影响任何变量的值。而如果 node. 引用通过 . 的方式,那么他的值就有变化的可能。
警惕引用丢失和内存泄漏
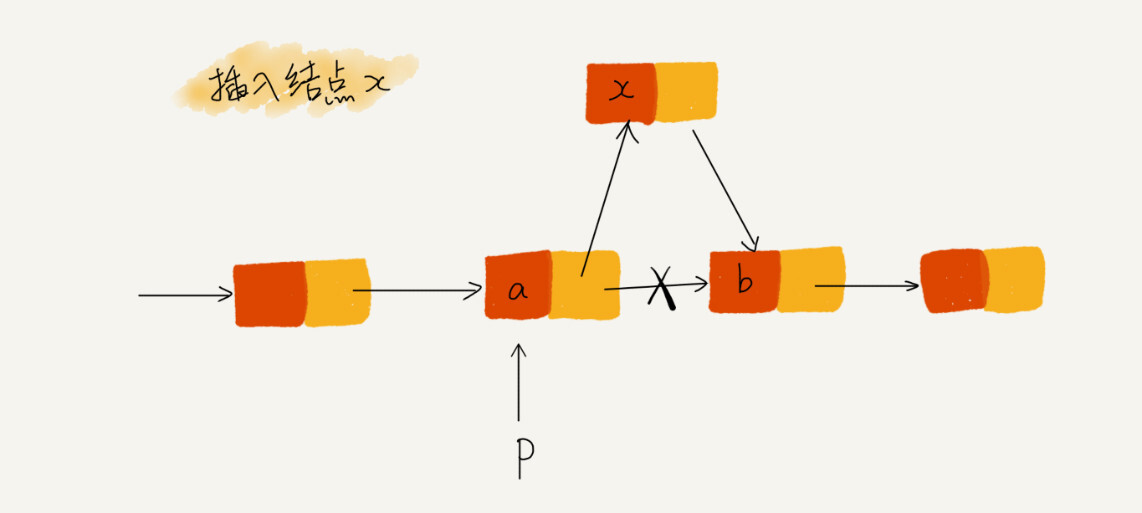
比如链表插入节点操作。
1
2
| Node targetNode = new Node(null, 1);
Node preNode;
|
错误示范:
1
2
| preNode.next = targetNode;
targeNode.next = preNode.next.next;
|
这里现将前节点指向目标节点,然后目标节点再指向前节点的下下个节点,意思是没有错误,但是会导致后节点以及之后都会被丢失。
正确的做法应该是:
1
2
| targetNode.next = preNode.next.next;
preNode.next = targeNode;
|
虽然仅仅是调换了顺序,就会产生不同的结果。同样删除节点时,也要记得手动释放内存。
利用哨兵简化实现难度
针对链表的插入、删除操作,需要对插入第一个结点和删除最后一个结点的情况进行特殊处理。
重点留意边界条件处理
- 如果链表为空,代码是否能正常工作
- 如果链表只包含一个节点,代码是否能正常工作
- 如果链表只包含两个节点,代码是否能正常工作
- 代码逻辑在处理头结点和尾节点的时候,代码是否能正常工作
举例画图,辅助思考
我平常在做练习题时,身边必备一张纸和一纸笔,对特殊的逻辑进行画图举例演示,很大程度上可以帮助自己理清逻辑。
多写多练
多多练习吧!
下面写几个练习题
代码实现单链列表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
| class SinglyLinkedList {
private Node head = null;
void insertToHead(Node node) {
if (head == null) {
head = node;
} else {
node.next = head;
head = node;
}
System.out.println("insert head " + node.value + " data:\t" + toString());
}
void insertToHead(int value) {
insertToHead(createNode(value));
}
void insertAfter(Node node, Node newNode) {
if (node == null) return;
newNode.next = node.next;
node.next = newNode;
System.out.println("insertAfter data:\t" + toString());
}
void insertAfter(Node node, int value) {
insertAfter(node, createNode(value));
}
void insertBefore(Node before, Node newNode) {
if (before == null) return;
if (head == before) {
insertToHead(newNode);
return;
}
Node temp = head;
while (temp != null && temp.next != before) {
temp = temp.next;
}
newNode.next = before;
temp.next = newNode;
System.out.println("insertBefore data:\t" + toString());
}
void insertBefore(Node before, int value) {
insertBefore(before, createNode(value));
}
Node findByValue(int value) {
Node temp = head;
while (temp != null && temp.value != value) {
temp = temp.next;
}
return temp;
}
Node findByIndex(int index) {
Node temp = head;
int pos = 0;
while (temp != null && pos != index) {
temp = temp.next;
pos++;
}
return temp;
}
void insertLast(Node node) {
if (head == null) {
head = node;
System.out.println("insert last " + node.value + " data:\t" + toString());
return;
}
Node temp = head;
while (temp.next != null) {
temp = temp.next;
}
temp.next = node;
System.out.println("insert last " + node.value + " data:\t" + toString());
}
void insertLast(int value) {
insertLast(createNode(value));
}
private Node createNode(int value) {
return new Node(null, value);
}
void deleteByValue(int value) {
if (head == null) {
return;
}
Node before = null;
Node current = head;
while (current != null && current.value != value) {
before = current;
current = current.next;
}
if (current == null) {
return;
}
if (before == null) {
head = head.next;
} else {
before.next = current.next;
}
System.out.println("deleteByValue:\t" + toString());
}
void deleteByNode(Node node) {
if (head == null || node == null) {
return;
}
Node temp = head;
while (temp != null && temp.next != node) {
temp = temp.next;
}
temp.next = node.next;
System.out.println("deleteByNode:\t" + toString());
}
@Override
public String toString() {
Node temp = head;
StringBuilder sb = new StringBuilder();
sb.append("[");
while (temp != null) {
sb.append(temp.value).append(",");
temp = temp.next;
}
sb.append("]");
return sb.toString();
}
static class Node {
int value;
Node next;
Node(Node next, int value) {
this.next = next;
this.value = value;
}
int getData() {
return value;
}
}
public static void main(String[] args) {
SinglyLinkedList linkedList = new SinglyLinkedList();
linkedList.insertLast(1);
linkedList.insertLast(2);
linkedList.insertLast(3);
linkedList.insertLast(4);
linkedList.insertToHead(5);
linkedList.insertAfter(linkedList.findByValue(3), 6);
linkedList.insertBefore(linkedList.findByValue(1), 7);
linkedList.deleteByValue(2);
linkedList.deleteByNode(linkedList.findByValue(1));
}
}
|
输出结果:
1
2
3
4
5
6
7
8
9
| insert last 1 data: [1,]
insert last 2 data: [1,2,]
insert last 3 data: [1,2,3,]
insert last 4 data: [1,2,3,4,]
insert head 5 data: [5,1,2,3,4,]
insertAfter data: [5,1,2,3,6,4,]
insertBefore data: [5,7,1,2,3,6,4,]
deleteByValue: [5,7,1,3,6,4,]
deleteByNode: [5,7,3,6,4,]
|
判断是否为回文数
核心思想:使用两个指针,一个慢指针,每次移动一个节点,一个快指针,每次移动两个节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| private boolean isPalindrome() {
if (head == null || head.next == null) {
return false;
}
Node pre = null;
Node slow = head;
Node fast = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
Node temp = slow.next;
slow.next = pre;
pre = slow;
slow = temp;
}
if (fast != null) {
slow = slow.next;
}
while (slow != null && pre != null) {
if (slow.value != pre.value) {
return false;
}
slow = slow.next;
pre = pre.next;
}
return true;
}
|
输出结果
1
2
3
4
5
| insert last 1 data: [1,]
insert last 2 data: [1,2,]
insert last 2 data: [1,2,2,]
insert last 1 data: [1,2,2,1,]
是否为回文函数: true
|
节点回转
核心思想:每次遍历时,回转节点的逻辑操作顺序,且看代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| private static Node reversed(Node node) {
if (node.next == null) {
return node;
}
Node pre = null;
while (node != null) {
Node temp = node.next;
node.next = pre;
pre = node;
node = temp;
}
return pre;
}
|
输出结果:
判断是否是循环节点
核心思想:循环节点的特点就在于链表的尾部指向头部,只需要是用快慢节点进行遍历,如果不是循环节点,循环一次就结束了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
private static boolean isCircle(Node node) {
int count = 0;
Node slow = node;
Node fast = node;
while (slow != null && fast != null && fast.next != null) {
count++;
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
System.out.println("循环了 " + count + "次");
return true;
}
}
System.out.println("循环了 " + count + "次");
return false;
}
|
输出结果
拼接两个有序节点
核心思想:首先创建一个空的头节点,然后两个有序链表依次遍历,谁小就把这个空节点指向谁(默认从小到大排序)。其中需要注意的是,如果一个节点提前结束了,那么就需要将新节点直接指向剩下的那个节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| private static Node mergeNode(Node aNode, Node bNode) {
Node head = new Node(null, -1);
Node tail = head;
if (aNode == null) {
head = bNode;
}
if (bNode == null) {
head = aNode;
}
while (aNode != null && bNode != null) {
if (aNode.value > bNode.value) {
tail.next = bNode;
bNode = bNode.next;
} else {
tail.next = aNode;
aNode = aNode.next;
}
tail = tail.next;
}
if (aNode == null) {
tail.next = bNode;
}
if (bNode == null) {
tail.next = aNode;
}
if (head == null) {
return null;
}
return head.next;
}
|
输出结果:
1
2
3
4
5
| A 节点: 135
B 节点: 24689
12345689
|
删除倒数第 N 个节点
核心思想:快慢指针,快的比慢 的多 N 个,遍历到最后,慢节点指向倒数第 N 个节点,然后直接进行删除。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
private static void deleteLast(Node node, int n) {
int count = 0;
Node head = node;
while (head != null) {
count ++;
head = head.next;
}
if (n > count) {
return;
}
if (n == count) {
if (n == 1) {
node.next = null;
} else {
node.value = node.next.value;
node.next = node.next.next;
}
return;
}
Node slow = node;
Node fast = node;
int tempCount = 0;
while (slow != null && fast.next != null) {
if (tempCount < n) {
tempCount ++;
} else {
slow = slow.next;
}
fast = fast.next;
}
slow.next = slow.next.next;
}
|
输出结果:
找出中间节点
核心思想:直接使用快慢指针进行遍历,慢指针每次移动一个,快指针每次移动两个。
1
2
3
4
5
6
7
8
9
| private static int findMiddleNode(Node node) {
Node fast = node;
Node slow = node;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow.value;
}
|
输出结果:
参考自极客时间





